• Konvolucijski modeli
• Vježba
  • 1. zadatak
  • 2. zadatak
  • 3. zadatak
  • 4. zadatak
• Dodatni materijali

2. vježba: konvolucijski modeli (CNN)

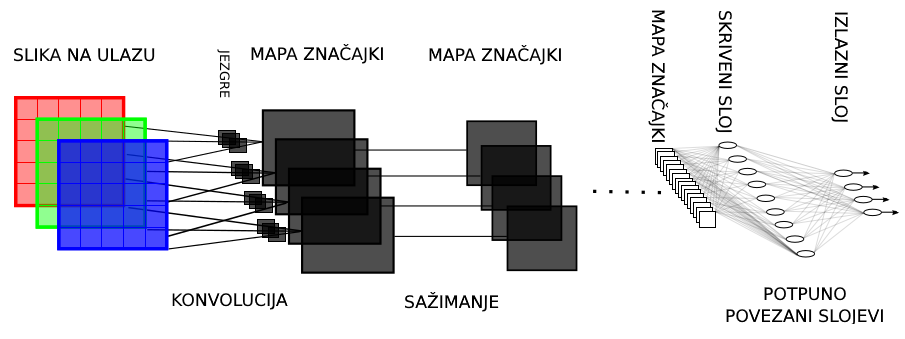
U ovoj vježbi bavimo se konvolucijskim modelima. Ti modeli prikladni su za obradu podataka s topologijom rešetke, gdje je osobito važno ostvariti kovarijantnost na translaciju. Dobar primjer takvih podataka su tipične RGB slike u kojima se isti objekt može pojaviti na mnogim prostornim lokacijama. Potpuno povezani slojevi nisu prikladni za analizu takvih slika jer svaka aktivacija ovisi o svim pikselima i tako od šume ne vidi stabla. Takav pristup bi ohrabrivao specijalizaciju aktivacija na pojedine dijelove slike, što bi značilo da bi model morao odvojeno učiti kako jedan te isti objekt izgleda u različitim dijelovima slike. Takva situacija pogodovala bi prenaučenosti, odnosno vodila bi na lošu generalizaciju. Osim toga dodatni problem je što slike tipično sadrže puno piksela. Na primjer, prosječne dimenzije slike iz poznatog skupa ImageNet iznose 3x200x200 što znači da bi svaka aktivacija iz prvog sloja trebala imati 3*200*200=120,000 težina. Takva situacija je neodrživa jer je broj parametara ograničen memorijom GPU-a.

Vidimo da bi puno bolje za nas bilo kad bi svaka aktivacija bila lokalno povezana s malenim susjedstvom prethodnog sloja, jer bi to uvelike smanjilo broj težina. Aktivacije u ranim slojevima imale bi malo receptivno polje i mogle bi modelirati samo jednostavne značajke koje bi detektirale jednostavne uzorke poput linija i rubova. Kasniji slojevi hijerarhijski bi gradili sve kompleksnije i kompleksnije značajke koje bi imale sve veće i veće receptivno polje. Nadalje, kovarijantnost na translacije unutar slike mogli bismo ostvariti dijeljenjem parametara aktivacija na različitim prostornim lokacijama. U takvoj organizaciji, latentne aktivacije sadrže izlaz istog podmodela na različitim lokacijama slike. Težine konvolucijskih slojeva obično nazivamo filtrima. Svaki filtar definira afinu transformaciju malenog lokalnog susjedstva prethodnog sloja koja se naknadno ulančava s nelinearnom aktivacijskom funkcijom. Tipično, lokalno susjedstvo filtra ima kvadratni oblik k✕k, k ∈ {3,5,7}, a nelinearnost je zglobnica. Da zaključimo, konvolucijski modeli koriste tri važne ideje: rijetku povezanost, dijeljenje parametara i ekvivarijantnost reprezentacije.

Primjer konvolucijskog modela za klasifikaciju slika. Tipično se izmjenjuju konvolucijski slojevi i slojevi sažimanja. Na kraju se dolazi do vektora značajki koji se potpuno povezanim slojem preslikava u konačnu kategoričku distribuciju preko poznatih razreda. Slika je preuzeta iz diplomskog rada Vedrana Vukotića.

Vježba

Kod za prva dva zadatka nalazi se ovdje. Biblioteke koje su vam potrebne za ovu vježbu su PyTorch, torchvision, NumPy, Cython, matplotlib i scikit-image. Module Pythona najlakše je povući iz pipa. Druga opcija je koristiti distribucijske pakete. Pazite da odaberete verzije za Python 3.

U datoteci layers.py nalaze se definicije slojeva od kojih se mogu graditi duboki konvolucijski modeli. Svaki sloj sadrži tri metode potrebne za izvođenje algoritma backprop. Metoda forward izvodi unaprijedni prolazak kroz sloj i vraća rezultat. Metode backward_inputs i backward_params izvode unatražni prolaz. Metoda backward_inputs računa gradijent s obzirom na ulazne podatke (\( \frac{∂L}{∂\mathbf{x}} \) gdje je \(\mathbf{x}\) ulaz u sloj). Metoda backward_params računa gradijent s obzirom na parametre sloja (\( \frac{∂L}{∂\mathbf{w}} \) gdje vektor \(\mathbf{w}\) vektor predstavlja sve parametre sloja)).

1. zadatak (25%)

Dovršite implementacije potpuno povezanog sloja, sloja nelinearnosti te funkcije gubitka u razredima FC, ReLU i SoftmaxCrossEntropyWithLogits. Podsjetimo se, gubitak unakrsne entropije računa udaljenost između točne distribucije i distribucije koju predviđa model i definiran je kao:

U prikazanoj jednadžbi C predstavlja broj razreda, a \( \mathbf{x} \) ulaz funkcije softmaks kojeg možemo zvati klasifikacijska mjera ili logit. Vektor \( \mathbf{y} \) sadrži točnu distribuciju preko svih razreda za dani primjer. Tu distribuciju najčešće zadajemo jednojediničnim (eng. one-hot) vektorom. Skalar \( p_j = \text{softmax}_j(\mathbf{x}) \) predstavlja izlaz funkcije softmax za razred \(j\). Radi jednostavnosti, jednadžba prikazuje gubitak za samo jedan primjer, dok ćemo u praksi obično razmatrati prosječan gubitak preko svih primjera mini-grupe. Da biste izveli unatražni prolazak kroz sloj potrebno je najprije izračunati gradijent gubitka s obzirom na logite \( \frac{∂L}{∂\mathbf{x}} \). Izvod možemo pojednostavniti tako da unaprijed raspišemo funkciju softmax:

Sada možemo jednostavno izračunati derivaciju funkcije cilja s obzirom na k-ti logit \( x_k \):

Konačno, gradijent s obzirom na sve logite dobivamo kao vektorsku razliku između
predikcije modela i točne distribucije:

Kako biste bili sigurni da ste ispravno napisali sve slojeve testirajte gradijente pozivom skripte check_grads.py. Zadovoljavajuća relativna greška bi trebala biti manja od \(10^{-5}\) ako vaši tenzori imaju dvostruku preciznost. Proučite izvorni kod te skripte jer će vam ta funkcionalnost biti vrlo korisna za treću vježbu. Razmislite zašto pri učenju dubokih modela radije koristimo analitičke nego numeričke gradijente.

Sada prevedite Cython modul im2col_cython.pyx pozivom python3 setup_cython.py build_ext --inplace te po potrebi izmijenite varijable DATA_DIR i SAVE_DIR. Proučite izvorni kod funkcija col2im_cython i im2col_cython te istražite kako se te funkcije koriste.

Proučite i skicirajte model zadan objektom net u skripti train.py. Odredite veličine tenzora te broj parametara u svakom sloju. Odredite veličinu receptivnog polja značajki iz posljednjeg (drugog) konvolucijskog sloja. Procijenite ukupnu količinu memorije za pohranjivanje aktivacija koje su potrebne za provođenje backpropa ako učimo s mini-grupama od 50 slika.

Napokon, pokrenite učenje modela pozivom skripte train.py. Odredite vezu između početnog iznosa funkcije gubitka i broja razreda C. Tijekom učenja možete promatrati vizualizaciju filtara koji se spremaju u kazalo SAVE_DIR. Budući da svaka težina odgovara jednom pikselu slike, u vašem pregledniku isključite automatsko glađenje slike. Preporuka je da na Linuxu koristite preglednik Geeqie.

2. zadatak (25%)

U ovom zadatku trebate dodati podršku za L2 regularizaciju parametara. Dovršite implementaciju sloja L2Regularizer te naučite regularizirani model iz prethodnog zadatka koji se nalazi u train_l2reg.py. Proučite efekte regularizacijskog hiper-parametra tako da naučite tri različita modela s \( \lambda = 1e^{-3}, \lambda=1e^{-2}, \lambda=1e^{-1} \) te usporedite naučene filtre u prvom sloju i dobivenu točnost.

Slučajno inicijalizirani filtri u prvom sloju na početku učenja (iznad) i naučeni filtri (ispod) s regularizacijom lambda = 0.01.

3. zadatak - usporedba s PyTorchem (25%)

U PyTorchu definirajte i naučite model koji je ekvivalentan regulariziranom modelu iz 2. zadatka. Koristite identičnu arhitekturu i parametre učenja da biste reproducirali rezultate. Konvoluciju zadajte operacijama torch.nn.Conv2d ili torch.nn.functional.conv2d. U nastavku teksta navodimo primjer korištenja konvolucije razredom torch.nn.Conv2d.

import torch
from torch import nn
 
class CovolutionalModel(nn.Module):
  def __init__(self, in_channels, conv1_width, ..., fc1_width, class_count):
    self.conv1 = nn.Conv2d(in_channels, conv1_width, kernel_size=5, stride=1, padding=2, bias=True)
    # ostatak konvolucijskih slojeva i slojeva sažimanja
    ...
    # potpuno povezani slojevi
    self.fc1 = nn.Linear(..., fc1_width, bias=True)
    self.fc_logits = nn.Linear(fc1_width, class_count, bias=True)

    # parametri su već inicijalizirani pozivima Conv2d i Linear
    # ali možemo ih drugačije inicijalizirati
    self.reset_parameters()

  def reset_parameters(self)
    for m in self.modules():
      if isinstance(m, nn.Conv2d):
        nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')
        nn.init.constant_(m.bias, 0)
      elif isinstance(m, nn.Linear) and m is not self.fc_logits:
        nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')
        nn.init.constant_(m.bias, 0)
    self.fc_logits.reset_parameters()

  def forward(self, x):
    h = self.conv1(x)
    ...
    h = torch.relu(h)  # može i h.relu() ili nn.functional.relu(h)
    ...
    h = h.view(h.shape[0], -1)
    h = self.fc1(h)
    h = torch.relu(h)
    logits = self.fc_logits(h)
    return logits

Ako želite koristiti torch.nn.functional.conv2d, vodite računa o ručnom definiranju parametara tipa torch.nn.Parameter. Pritom se poslužite slijedećim primjerom. Vodite računa o odgovarajućoj dimenzionalnosti tenzora konvolucijskih jezgara te tenzora pomaka.

Tijekom učenja vizualizirajte filtre u prvom sloju kao u prethodnoj vježbi. Nakon svake epohe učenja pohranite filtre i gubitak u datoteku (ili koristite Tensorboard).

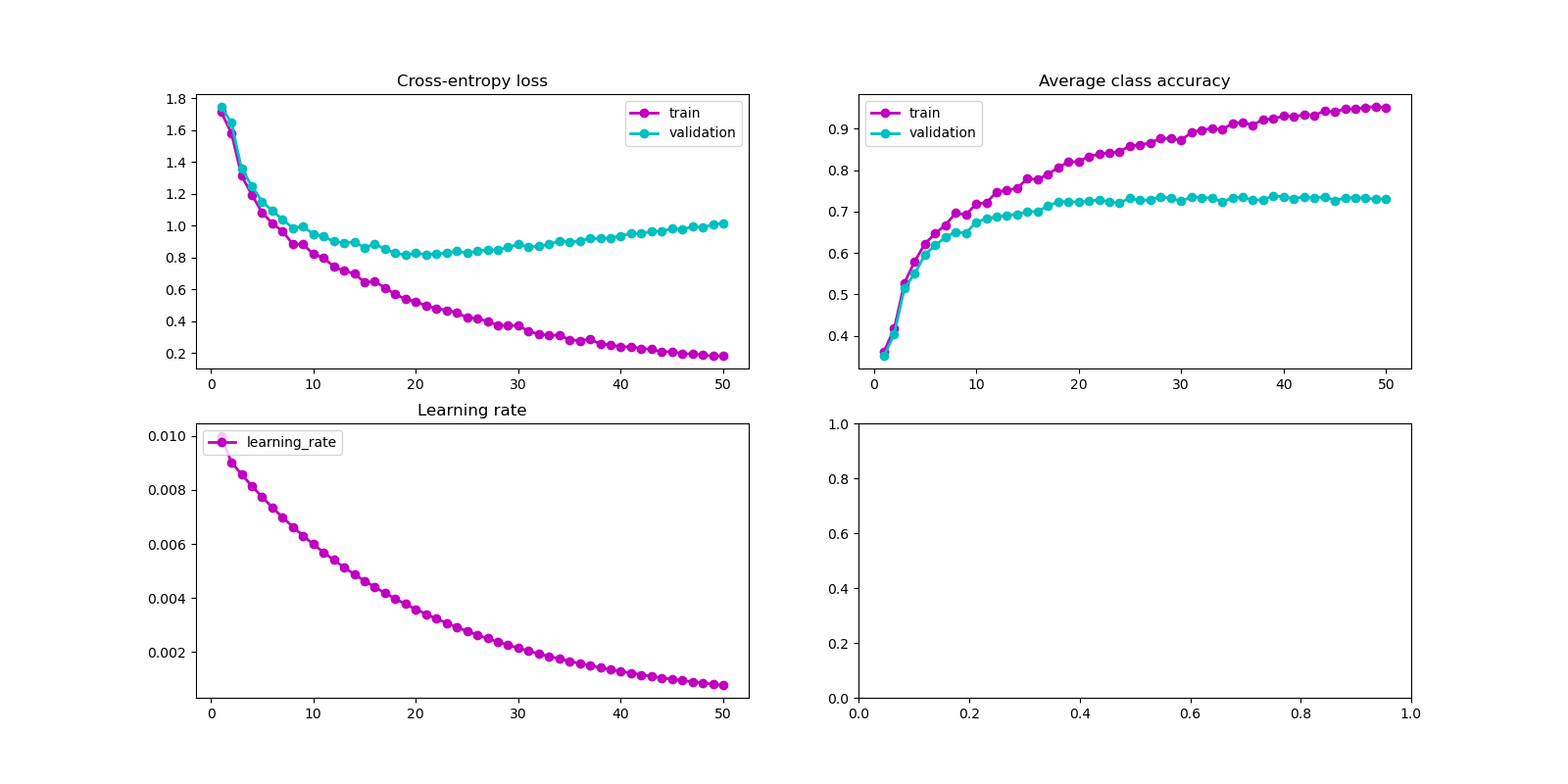
Na kraju učenja prikažite kretanje gubitka kroz epohe (Matplotlib).

Za razliku od 1. vježbe, ovdje za iteriranje i uzorkovanje mini-grupa preporučamo koristiti torch.utils.data.DataLoader prema sljedećoj dokumentaciji.

4. zadatak - Klasifikacija na skupu CIFAR-10 (25%)

Skup podataka CIFAR-10 sastoji se od 50000 slika za učenje i validaciju te 10000 slika za testiranje dimenzija 32x32 podijeljenih u 10 razreda. Najprije skinite dataset pripremljen za Python odavde ili korištenjem torchvision.datasets.CIFAR10. Možete iskoristiti sljedeći kod kako biste učitali podatke i pripremili ih.

import os
import pickle
import numpy as np

def shuffle_data(data_x, data_y):
  indices = np.arange(data_x.shape[0])
  np.random.shuffle(indices)
  shuffled_data_x = np.ascontiguousarray(data_x[indices])
  shuffled_data_y = np.ascontiguousarray(data_y[indices])
  return shuffled_data_x, shuffled_data_y

def unpickle(file):
  fo = open(file, 'rb')
  dict = pickle.load(fo, encoding='latin1')
  fo.close()
  return dict

DATA_DIR = '/path/to/data/'

img_height = 32
img_width = 32
num_channels = 3
num_classes = 10

train_x = np.ndarray((0, img_height * img_width * num_channels), dtype=np.float32)
train_y = []
for i in range(1, 6):
  subset = unpickle(os.path.join(DATA_DIR, 'data_batch_%d' % i))
  train_x = np.vstack((train_x, subset['data']))
  train_y += subset['labels']
train_x = train_x.reshape((-1, num_channels, img_height, img_width)).transpose(0, 2, 3, 1)
train_y = np.array(train_y, dtype=np.int32)

subset = unpickle(os.path.join(DATA_DIR, 'test_batch'))
test_x = subset['data'].reshape((-1, num_channels, img_height, img_width)).transpose(0, 2, 3, 1).astype(np.float32)
test_y = np.array(subset['labels'], dtype=np.int32)

valid_size = 5000
train_x, train_y = shuffle_data(train_x, train_y)
valid_x = train_x[:valid_size, ...]
valid_y = train_y[:valid_size, ...]
train_x = train_x[valid_size:, ...]
train_y = train_y[valid_size:, ...]
data_mean = train_x.mean((0, 1, 2))
data_std = train_x.std((0, 1, 2))

train_x = (train_x - data_mean) / data_std
valid_x = (valid_x - data_mean) / data_std
test_x = (test_x - data_mean) / data_std

train_x = train_x.transpose(0, 3, 1, 2)
valid_x = valid_x.transpose(0, 3, 1, 2)
test_x = test_x.transpose(0, 3, 1, 2)

Vaš zadatak je da u PyTorchu naučite konvolucijski model na ovom skupu. U nastavku je prijedlog jednostavnog modela s kojom biste trebali dobiti ukupnu točnost oko 70% na validacijskom skupu:

conv(16,5) -> relu() -> pool(3,2) -> conv(32,5) -> relu() -> pool(3,2) -> fc(256) -> relu() -> fc(128) -> relu() -> fc(10)

gdje conv(16,5) predstavlja konvoluciju sa 16 mapa te dimenzijom filtra 5x5, a pool(3,2) max-pooling sloj s oknom veličine 3x3 i pomakom (stride) 2. Prilikom treniranja padajuću stopu učenja možete implementirati korištenjem torch.optim.lr_scheduler.ExponentialLR.

Napišite funkciju evaluate koja na temelju predviđenih i točnih indeksa razreda određuje pokazatelje klasifikacijske performanse: ukupnu točnost klasifikacije, matricu zabune (engl. confusion matrix) u kojoj retci odgovaraju točnim razredima a stupci predikcijama te mjere preciznosti i odziva pojedinih razreda. U implementaciji prvo izračunajte matricu zabune, a onda sve ostale pokazatelje na temelju nje. Tijekom učenja pozivajte funkciju evaluate nakon svake epohe na skupu za učenje i validacijskom skupu te na grafu pratite sljedeće vrijednosti: prosječnu vrijednost funkcije gubitka, stopu učenja te ukupnu točnost klasifikacije. Preporuka je da funkciji provedete samo unaprijedni prolaz kroz dane primjere koristeći torch.no_grad() i pritom izračunati matricu zabune. Pazite da slučajno ne pozovete i operaciju koja provodi učenje tijekom evaluacije. Na kraju funkcije možete izračunati ostale pokazatelje te ih isprintati.

Primjer grafa učenja za navedeni model uz veličinu grupe od 50

Vizualizirajte slučajno inicijalizirane težine konvolucijskog sloja možeze dohvatiti korištenjem conv.weight. U nastavku je primjer kako to može izgledati, ovisno o načinu implementacije konvolucijske mreže.

net = ConvNet()

draw_conv_filters(0, 0, net.conv1.weight.detach().numpy(), SAVE_DIR)

U nastavku se nalazi kod koji možete koristiti za vizualizaciju:

def draw_conv_filters(epoch, step, weights, save_dir):
  w = weights.copy()
  num_filters = w.shape[0]
  num_channels = w.shape[1]
  k = w.shape[2]
  assert w.shape[3] == w.shape[2]
  w = w.transpose(2, 3, 1, 0)
  w -= w.min()
  w /= w.max()
  border = 1
  cols = 8
  rows = math.ceil(num_filters / cols)
  width = cols * k + (cols-1) * border
  height = rows * k + (rows-1) * border
  img = np.zeros([height, width, num_channels])
  for i in range(num_filters):
    r = int(i / cols) * (k + border)
    c = int(i % cols) * (k + border)
    img[r:r+k,c:c+k,:] = w[:,:,:,i]
  filename = 'epoch_%02d_step_%06d.png' % (epoch, step)
  ski.io.imsave(os.path.join(save_dir, filename), img)

CIFAR-10: slučajno inicijalizirani filtri u prvom sloju na početku učenja (iznad) i naučeni filtri (ispod) s regularizacijom lambda = 0.0001.

Prikažite 20 netočno klasificiranih slika s najvećim gubitkom te ispišite njihov točan razred, kao i 3 razreda za koje je model dao najveću vjerojatnost. Da biste prikazali sliku, morate najprije poništiti normalizaciju srednje vrijednosti i varijance:

import skimage as ski
import skimage.io

def draw_image(img, mean, std):
  img = img.transpose(1, 2, 0)
  img *= std
  img += mean
  img = img.astype(np.uint8)
  ski.io.imshow(img)
  ski.io.show()

Ispod se nalazi kod koji možete iskoristiti za crtanje grafova:

def plot_training_progress(save_dir, data):
  fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(16,8))

  linewidth = 2
  legend_size = 10
  train_color = 'm'
  val_color = 'c'

  num_points = len(data['train_loss'])
  x_data = np.linspace(1, num_points, num_points)
  ax1.set_title('Cross-entropy loss')
  ax1.plot(x_data, data['train_loss'], marker='o', color=train_color,
           linewidth=linewidth, linestyle='-', label='train')
  ax1.plot(x_data, data['valid_loss'], marker='o', color=val_color,
           linewidth=linewidth, linestyle='-', label='validation')
  ax1.legend(loc='upper right', fontsize=legend_size)
  ax2.set_title('Average class accuracy')
  ax2.plot(x_data, data['train_acc'], marker='o', color=train_color,
           linewidth=linewidth, linestyle='-', label='train')
  ax2.plot(x_data, data['valid_acc'], marker='o', color=val_color,
           linewidth=linewidth, linestyle='-', label='validation')
  ax2.legend(loc='upper left', fontsize=legend_size)
  ax3.set_title('Learning rate')
  ax3.plot(x_data, data['lr'], marker='o', color=train_color,
           linewidth=linewidth, linestyle='-', label='learning_rate')
  ax3.legend(loc='upper left', fontsize=legend_size)

  save_path = os.path.join(save_dir, 'training_plot.png')
  print('Plotting in: ', save_path)
  plt.savefig(save_path)

plot_data = {}
plot_data['train_loss'] = []
plot_data['valid_loss'] = []
plot_data['train_acc'] = []
plot_data['valid_acc'] = []
plot_data['lr'] = []

for epoch in range(num_epochs):
    X, Yoh = shuffle_data(train_x, train_labels)
    X = torch.FloatTensor(X)
    Yoh = torch.FloatTensor(Yoh)
    for batch in range(n_batch):
        # broj primjera djeljiv s veličinom grupe bsz
        batch_X = X[batch*bsz:(batch+1)*bsz, :]
        batch_Yoh = Yoh[batch*bsz:(batch+1)*bsz, :]

        loss = model.get_loss(batch_X, batch_Yoh)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

        if batch%100 == 0:
            print("epoch: {}, step: {}/{}, batch_loss: {}".format(epoch, batch, n_batch, loss))

        if batch%200 == 0:
            draw_conv_filters(epoch, batch, model.conv1.weight.detach().cpu().numpy(), SAVE_DIR)


    train_loss, train_acc = evaluate(model, train_x, train_labels)
    val_loss, val_acc = evaluate(model, valid_x, valid_labels)

    plot_data['train_loss'] += [train_loss]
    plot_data['valid_loss'] += [val_loss]
    plot_data['train_acc'] += [train_acc]
    plot_data['valid_acc'] += [val_acc]
    plot_data['lr'] += [lr_scheduler.get_lr()]
    lr_scheduler.step()

plot_training_progress(SAVE_DIR, plot_data)

Ukoliko imate GPU, možda će vam biti zanimljivo pokušati dobiti bolje rezultate s moćnijom arhitekturom. U tom slučaju ovdje možete pronaći pregled članaka koji imaju najbolje rezultate na ovom skupu. Kao što vidite trenutni state of the art je oko 96% ukupne točnosti. Dva važna trika koje koriste najbolje arhitekture su skaliranje slika na veću rezoluciju kako bi omogućili da prvi konvolucijski slojevi uče značajke jako niske razine te proširivanje skupa za učenje raznim modificiranjem slika (data jittering). Bez ovih trikova je jako teško preći preko 90% ukupne točnosti.

Bonus zadatak - Multiclass hinge loss (max 20%)

Ovaj zadatak razmatra učenje modela za slike iz CIFARA s alternativnom formulacijom gubitka koju nismo obradili na predavanjima. Cilj je zamijeniti unakrsnu entropiju višerazrednom inačicom gubitka zglobnice. Objašnjenje tog gubitka možete pronaći ovdje. Za sve bodove zadatak je potrebno riješiti primjenom osnovnih PyTorch operacija nad tenzorima te usporediti postignute rezultate.

Pomoć: sučelje nove funkcije gubitka moglo bi izgledati ovako:

def multiclass_hinge_loss(logits: torch.Tensor, target: torch.Tensor, delta=1.):  
    """
        Args:
            logits: torch.Tensor with shape (B, C), where B is batch size, and C is number of classes.
            target: torch.LongTensor with shape (B, ) representing ground truth labels.
            delta: Hyperparameter.
        Returns:
            Loss as scalar torch.Tensor.
    """

Rješenje možete započeti razdvajanjem izlaza posljednjeg potpuno povezanog sloja na vektor logita točnih razreda i matricu logita netočnih razreda. To možete provesti pozivom funkcije torch.masked_select, pri čemu masku zadajete regularnom odnosno invertiranom verzijom matrice s jednojediničnim oznakama podataka. Sada razliku između matrice logita netočnih razreda i vektora logita točnih razreda možemo izračunati običnim oduzimanjem, jer PyTorch automatski umnaža (eng. broadcast) operand nižeg reda. Pripazite da sve tenzore preoblikujete na ispravni oblik, jer funkcija torch.masked_select vraća tenzor prvog reda. Maksimum po elementima možete računati odgovarajućom varijantom funkcije torch.max.

Dodatni materijali

• Deep learning book
• CS231n Convolutional Neural Networks for Visual Recognition